Lösung 2:

Antwort: 21,9cm²

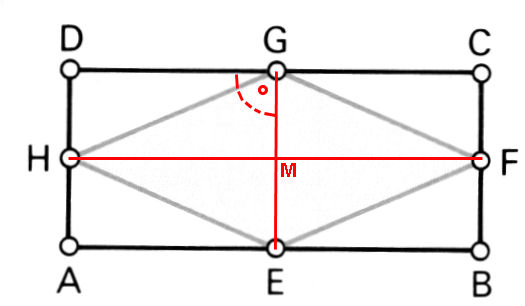
Da G und E die Mittelpunkte der entsprechenden Rechtecksseiten sind, entsteht bei G auch wieder ein rechter Winkel. Auch bei M ergibt sich einer, da in einer Raute die Diagonalen senkrecht aufeinander stehen.

DHMG ist somit ein Rechteck und seine Diagonale [HG] teilt es in zwei gleich große Teile. DHMG ist also exakt halb so groß wie das kleine Rechteck DHMG.

Die gleiche Überlegung gilt für die anderen drei kleinen Rechtecke. Damit kommt man zum Schluss, dass die Raute insgesamt exakt halb so groß sein muss wie das gesamte Rechteck.